home

author: niplav, created: 2024-04-22, modified: 2025-02-07, language: english, status: in progress, importance: 5, confidence: likely

In which to compare how similarly programs compute their outputs, naïvely and less naïvely.

Contents

Logical Correlation

Attention conservation notice: Premature formalization, ab-hoc mathematical definition.

Motivation, Briefly

In the twin prisoners dilemma, I cooperate with my twin because we're implementing the same algorithm. If we modify the twin slightly, for example to have a slightly longer right index-finger-nail, I would still cooperate, even though we're different algorithms, since little enough has been changed about our algorithms that the internal states and the output are basically the same.

It could be that I'm in a prisoner's dilemma with some program p^{\star} that, given some inputs, returns the same outputs as I do, but for completely different "reasons"—that is, the internal states are very different, and a slight change in input would cause the output to be radically different. Intuitively, my similarity to p^{\star} is pretty small, because even though it gives the same output, it gives that output for very different reasons, so I don't have much control over its outputs by controlling my own computations.

Let's call this similarity of two algorithms the logical correlation between the two algorithms (alternative terms "include “logical influence,” “logical correlation,” “correlation,” “quasi-causation,” “metacausation,” […] “entanglement”[,] “acausal influence”"). I take this term from Demski & Garrabrant 2020:

One idea is that exact copies should be treated as 100% under your “logical control”. For approximate models of you, or merely similar agents, control should drop off sharply as logical correlation decreases. But how does this work?

—Abram Demski & Scott Garrabrant, “Embedded Agency” p. 12, 2020

Similarly:

The reasoning behind cooperation does not involve a common cause of all collaborators' decisions. Instead, the correlation may be viewed as logical (Garrabrant et al., 2016): if I cooperate, then this implies that all other implementations of my decision algorithm also cooperate.

—Caspar Oesterheld, “Multiverse-wide Cooperation via Correlated Decision Making” p. 18, 2018

There isn't yet an established way of estimating the logical correlation between different decision algorithms.

A Naïve Formula

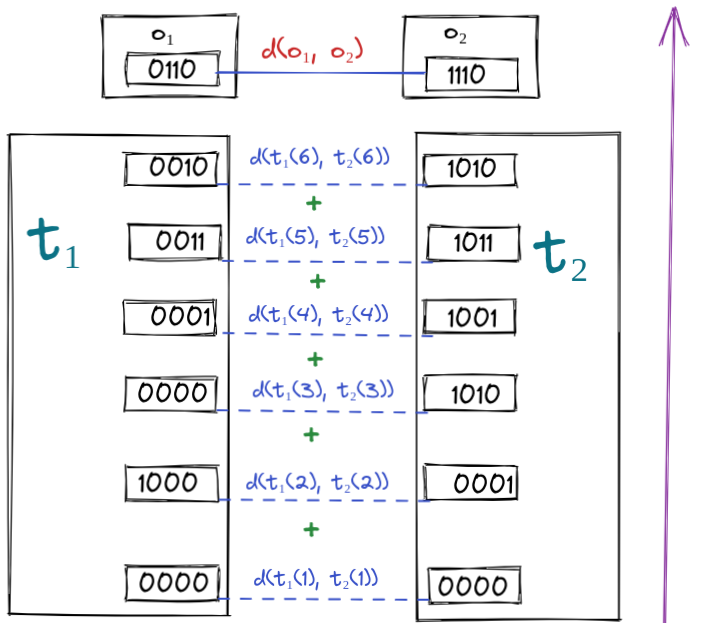
Thus: Consider the some naïve formula (which we'll designate by 合 1) for logical correlation2: Something that takes in two programs and returns a number that quantifies how similarly the two programs compute what they compute.

Setup

Let a program p be a tuple of code for a Turing machine and intermediate tape states after each command execution. We'll treat the final tape state as the output, all in binary.

That is p=(c, t) , with c \in \{0, 1\}^+ and t \in (\{0, 1\}^+)^+ . Let l=|t| be the number of steps that p takes to halt.

For simplicity's sake, let's give t[l] (the tape state upon halting) the name o , the output.

Possible Desiderata

  1. The type signature should be 合: P \rightarrow ℝ where P is the set of all possible programs for some Turing machine. 合 may potentially only map into a real interval, but I definitely want it to be a spectrum, which rules out many other notions of program similarity from computer science.
  2. If possible, we would want our formula for logical correlation to be a metric or a pseudometric on the space of programs:
    1. 合(p, p)=0 .
    2. Symmetry: 合(p_1, p_2)=合(p_2, p_1) .
    3. If p_1 \not=p_2 , then 合(p_1, p_2)>0 . This condition is dropped if we're fine with 合 being a pseudometric.
    4. The triangle inequality: 合(p_1, p_3) \le 合(p_1, p_2)+合(p_2, p_3) .
  3. If p_1 and p_2 have very similar outputs, and p_3 has a very different output, then 合(p_1, p_2)<合(p_1, p_3) (and 合(p_1, p_2)<合(p_2, p_3) ).
    1. I'm not so sure about this one: Let's say there's p , which outputs a binary string o \in \{0, 1\} , and p^{\not \sim} , which computes o in a completely different way, as well as p^{\lnot} , which first runs p , and then flips every bit on the tape, finally returning the negation of o . In this case, it seems that if p is a decision algorithm, it has far more "control" over the output of p^{\lnot} than over p^{\not \sim} .
    2. For the time being, I'm going to accept this, though ideally there'd be some way of handling the tradeoff between "computed the same output in a different way" and "computed a different output in a similar way".

Formal Definition

Let p_1=(c_1, t_1), p_2=(c_2, t_2) be two halting programs, l_1, l_2 are the number of steps it takes p_1, p_2 to halt, and o_1=t_{l_1}, o_2=t_{l_2} the last tape states (outputs) of the two programs.

Then a formula for the logical correlation 合 of p_1, p_2 , a tape-state discount factor γ 3, and a string-distance metric d: \{0, 1\}^+ \times \{0, 1\}^+ \rightarrow ℕ could be

合(p_1, p_2, γ)=d(o_1, o_2)+1-\exp(-\sum_{k=1}^{\min(l_1, l_2)} γ^k \cdot d(t_1[l_1-k], t_2[l_2-k]))

The lower 合 , the higher the logical correlation between p_1 and p_2 .

Explanation

Let's take a look at the equation again, but this time with some color highlighting:

合(p_1, p_2, γ)=\color{red}{d(o_1, o_2)}+1\color{orange}{-}\exp(-\color{green}{\sum_{k=1}^{\min(l_1, l_2)}} \color{purple}{γ^k \cdot} \color{blue}{d(t_1[l_1-k], t_2[l_2-k])})

The fundamental idea is that we first compute the distance of the two outputs. We then go backward through the trace of the two programs, adding up the pairwise differences of the traces at each timestep, potentially discounting the differences the farther they lie in in the "past" of the output/further towards the start of the computation.

Finally, we subtract the inverse of this (discounted) sum of trace differences from the output difference4.

The value of the exponential function here can maximally be 1 (since the smallest value of the sum is zero) and will always be greater than zero. Thus, since we're subtracting a number ≤1 from d(o_1, o_2)+1 , the resulting logical correlation must be d(o_1, o_2)≤合(p_1, p_2, γ)≤d(o_1, o_2)+1-ε . That implies that for three programs with the same output, their logical correlations all lie in that range. That also means that if d(o_1, o_2)<d(o_1, o_3) , then it's the case that 合(p_1, p_2, γ)<合(p_1, p_3, γ) .

Or, in even simpler terms; "Output similarity dominates trace similarity."

Different Trace Lengths

One might also want to be able to deal with the fact that programs have different trace lengths, and penalize that, e.g. amending the formula:

合'(p_1, p_2, γ)=合(p_1, p_2, γ)+2^{|l_1-l_2|}

Desiderata Fulfilled?

Does this fulfill our desiderata from earlier? I'll assume that the string distance d is a metric, in the mathematical sense.

Proving 合(p, p)=0

Proof:

d(o, o)+1-\exp(-\sum_{k=1}^{\min(l, l)} γ^k \cdot d(t(l-k), t(l-k)))= \\ 0+1-\exp(-\sum_{k=1}^l y^k \cdot 0)= \\ 1-\exp(0)= \\ 0

Since d is a metric, d(o, o)=0 .

Proving Symmetry

Symmetry is trivially true if we assume that d is symmetric.

Proving Positivity

The minimal logical correlation is 0.

合(p_1, p_2, γ) ≥ 0 \Leftrightarrow \\ d(o_1, o_2)+1-\exp(-\sum_{k=1}^{\min(l_1, l_2)} γ^k \cdot d(t_1[l_1-k], t_2[l_2-k])) ≥ 0 \Leftrightarrow \\ d(o_1, o_2)+1 ≥ \exp(-\sum_{k=1}^{\min(l_1, l_2)} γ^k \cdot d(t_1[l_1-k], t_2[l_2-k])) \Leftrightarrow \\ \ln(d(o_1, o_2)+1) + \sum_{k=1}^{\min(l_1, l_2)} γ^k \cdot d(t_1[l_1-k], t_2[l_2-k]) ≥ 0

This is true, because:

  1. d(o_1, o_2)≥0 , hence d(o_1, o_2)+1≥1 and thus \ln(d(o_1, o_2)+1)≥0 .
  2. d(t_1[l_1-k], t_2[l_2-k])≥0 for every k (since d is a metric).
  3. γ^k≥0 for every k .

Thus we have a sum of products of only positive things, which is in turn positive itself.

Only A Pseudometric

But, unfortunately, it isn't the case that if p_1≠p_2 , then 合(p_1, p_2, γ)>0 . Thus 合 is only a pseudometric.

Consider, for example, two programs that both write a 1 to the starting position on the tape and then halt, but with the difference that p_1 moves left and then right in the first two steps, and p_2 moves right and then left in the first two steps. Both programs have the same tape-state trace, but are not "equal" in the strict sense as they have different source codes.

You might now complain that this is vacuous, since the two programs have no relevant functional difference. That's true, but I suspect there's some trickier edge cases here where randomly initialized tapes can have very different (or in other cases equal) tape-state traces. If you find an equivalence class of programs that are just vacuously different, I'd be interested in hearing about it.

A Less Naïve Formula

I think that the naïve formula is too naïve. Reasons:

  1. If you have a program p and a program p^- which is just p but with the tape reversed (so that whenever p makes a step left, p^- makes a step right, and same with right steps for p ). Intuitively p and p^- should have a very high logical correlation, but 合 would tell us that they very much don't.
  2. 合 doesn't really make a statement about which states of the program influence which other states, it just compares them.
  3. I'm a bit unhappy that the code doesn't factor into 合 , and ideally one would want to be able to compute the logical correlation without having to run the program.

I think one can create a better (though not perfect) way of determining logical correlations based on (something like) Shapley Values and possible tape-permutations.

Explanation

We'll inherit the basic setup from the naïve formula, but now we won't determine the logical correlation of the whole outputs o_1, o_2 . Instead we pick one bit from each output, say b_1=o_1[k], b_2=o_2[k] for some k \in ℕ .

This formula is based on the assumption that Shapley values of tape cells over time are a kind of fingerprint of the program as it runs, and as such can be compared with some distance function akin to d in the naïve formula.

Shapley Values for Tape States

We treat each tape state t_i of a Turing machine as a set of players, which can play either 0 or 1 (the two states each cell on the tape can assume).

Then we compute the Shapley value for each tape state on the bit produced down the line by the Turing machine. To recap, the Shapley value assumes that there's a set t_i(j) (with j \in ℕ ) of players, and a function v: 2^{t_i(j)} \rightarrow \{0,1\} for all subsets of players—in this case the execution of the program from t_i until it halts. It's assumed that v(\emptyset)=0 .

People sometimes like to claim that the Shapley value is some kind of Platonic ideal of measuring contribution. I don't know about that, but it has some nice properties that uniquely identify it.

The Shapley value for a player j is then computed with the following equation:

\phi_j(v)=\sum_{S \subseteq N \backslash \{j\}} \frac{|S|!(n-|S|-1)!}{n!} (v(S \cup\{j\})-v(S)))

Two conceptual difficulties present themselves:

  1. The Shapley value assumes there's a null-action for each player, i.e. players can choose not to do anything,
  2. At different times different programs on the same Turing machine can have accessed different parts of the tape—in the most extreme case, one program just moves one tape to the left, and stays there, while the other program runs off along tapes to the right. In those cases, we get differently sized "lists" of influence-values.

1. can be solved by setting the null action to the tapestate produced by the program preceding the tapestate. I imagine this as a tapestate being able to "decide" to flip to the opposite bit before the program resumes, which counts as participating. We'll designate the function of letting a program p continue running from a timestep k until halting as \bar{p}_k .

(Note that it can very well be the case that a cell flipping its tape bit can have a negative Shapley value, e.g. if the output bit is one if the input bit does nothing, and zero if the input bit is flipped. This felt like a problem to me for a while, but now I would guess it's not an issue, and is just a genuine behavior of the program that can be compared to the other one. I continue feeling a bit confused about whether there's something worth fixing here.)

For 2., my best solution is to be (overly?) expansive in which tape cells are considered as potential contributions: Let's call the "leftmost" tape cell reached by a program on a Turing machine during the whole execution f^{\leftarrow} and the "rightmost" one f^{\rightarrow} ( f for "frontier").

Then the subrange indexed of the whole tape is a range of natural numbers [\min(f^{\leftarrow}_1, f^{\leftarrow}_2), \dots, \max(f^{\rightarrow}_1, f^{\rightarrow}_2)] , abbreviated as f^{\leftrightarrow} .

Cells that haven't been "reached" yet by the program (or never will) automatically have a Shapley value of 0, that just falls out of the formula.5 Because we're taking the biggest possible "reached envelope" on the tape the tape segments for both programs have the same size.

So, for a bit b in the output of the program p , at some timestep k , we get a list of Shapley values:

ᖫ(p, t, k)=[\phi_j(\bar{p}_k): j \in f^{\leftrightarrow}]

We'll call ᖫ(p, t, k) the Shapley value profile of a program p at a timestep k .

Comparing Lists of Influences

ᖫ returns… a list of real numbers. So if we evaluate the Shapley value profile of two tape states for two different programs, we have to compare two same-length lists of real numbers and figure out how similar they are.

There are many ways to do so. I don't have a particular favorite, but for convience let's pretend we take the element-wise mean-squared error and call it a day.

I'll designate whatever difference measure is decided on as d , just as earlier.

Permuted Tapes

If we just use the difference between Shapley values for intermediate tape states, we won't have solved the first problem of the naïve formula: Direction-reversed programs are evaluated as being extremely dissimilar, even though they are very similar.

As hinted, I don't have a great solution to this, but my current best approach is to look at permutations of one of the tapes, and choose the one which best "matches up" the two Shapley value profiles with each other. E.g. for p, p^{-} from earlier we'd compare the two programs using the permutation that reverses the tape of p^{-} .

It's important that this permutation be chosen once for all timesteps.

I don't like this solution. Permutations are too permissive, and two programs where p_1 is best modeled as being pairwise flips of neighboring cells of p_2 are, intuitively, quite dissimilar.

My current best idea is to penalize permutations for complexity, e.g. by preferring permutations that can be constructed from few pairwise swappings (one generating set of the symmetric group). But that would strongly penalize "natural" very similar programs, such as p, p^{-} . If anyone here has good alternative ideas, hit me up.

Final Equation

Phew! That was a lot. Putting it all together, in a similar framework as with the naïve formula, yields6:

挧(p_1, p_2, b_1, b_2)=\color{red}{\mathbf{1}(b_1 \neq b_2)}+1-\color{blue}{\underset{\sigma \in \text{Sym}(f^{\leftrightarrow})}{\text{max }}} \exp(\color{orange}{-\sum_{k=1}^{\min(l_1, l_2)}} \color{grey}{d(}\color{blue}{\sigma(}\color{purple}{ᖫ(p_1, t_1, k)}\color{blue}{)}, \color{purple}{ᖫ(p_2, t_2, k)}\color{grey}{)}

with

ᖫ(p, t, k)=[\phi_j(\bar{p}_k): j \in f^{\leftrightarrow}]

If the two output bits are different, "start" with the logical correlation being 1. Go through the tape states backwards in terms of the two programs being run, back to the first "shared" program state. For each tape state, compute the Shapley value profile. Permute one Shapley value profile that it "best" matches up with the other one. Compute the difference of the Shapley value profiles, and sum them up.

The bigger the summed diffence, the smaller the exponent of the negative of that distance. The largest possible value of 挧 is 2-ε , the smallest possible value is 0—in cases where b_1=b_2 and the sum of differences is zero.

Remaining Problem: Time-Permuted Tapes

I see one clear indicator that this hasn't been ironed out yet: If p_1 computes an output by first computing the "left half" and then the "right half" (in terms of location on the tape relative to the starting position), and p_2 computes first the "right half" and then the "left half", but compute both halves in very similar ways, then they should be very logically correlated, but the less naïve formula will tell you that they're quite different. (Which is just a version of the tape permutation, but over runtime.)

I don't know how to account for time permutation without even more ugly hacks.

Other Ideas

The formulae I cobbled together are pretty specialized to Turing machines, and lack desired features. Some possible alternatives, which I'm not fond of for various reasons:

  1. Checking bisimilarity: Bisimilarity is a binary category: two programs either are bisimilar or they aren't. Logical correlation needs to be a spectrum so that one can tell which programs have higher & lower logical correlation with each other. At best, bisimilarity increases the space of programs that are surely highly logically correlated with another.
  2. Mutual information of the programs: If we allow the tapes to be initialized before running the programs, we can vary the initialized tape states and get two distributions of tape histories. From those two distributions one can calculate the mutual information. This solution has a lot going for it: It's simple to describe and mathematically beautiful, as well being safe to maximize. The two downsides I can think of for it are that (1) it's computationally costly to calculate, requiring a large number of samples of initializations of t[f^{\leftrightarrow}] , and that (2) it requires freely variable input parameters, but my æsthetic wants a method to compare two programs as static, unvariable objects. Still, if it turns out that mutual information of tape histories is the true name of logical correlation, I won't be surprised.
  3. Translate each program into a causal(?) graph and compare the graphs: I think that one can translate arbitrary programs into graph-like diagrams, and graphs can be compared (e.g. through graph edit distance, or by comparing the adjacency matrices or the Laplacian matrix and comparing the matrices. I haven't thought much about this option yet.

See Also

  1. Suggested by GPT-4. Stands for joining, combining, uniting. Also "to suit; to fit", "to have sexual intercourse", "to fight, to have a confrontation with", or "to be equivalent to, to add up". ↩

  2. Actually not explained in detail anywhere, as far as I can tell. ↩

  3. Which is needed because tape states close to the output are more important than tape states early on. ↩

  4. Together with adding one to avoid same logical correlations for programs with different outputs differences. ↩

  5. I have the suspicion that this whole thing isn't actually a problem and one can just compare permutations of the whole infinite tape, but I don't want to take any chances with weirdnesses around permutations of infinitely many elements, or the mean-squared error between infinitely long lists. Also it's nice to be able to actually implement the solution. ↩

  6. 挧 is a ghost character, and as such has no previously assigned meaning. ↩